Background Knowledge:

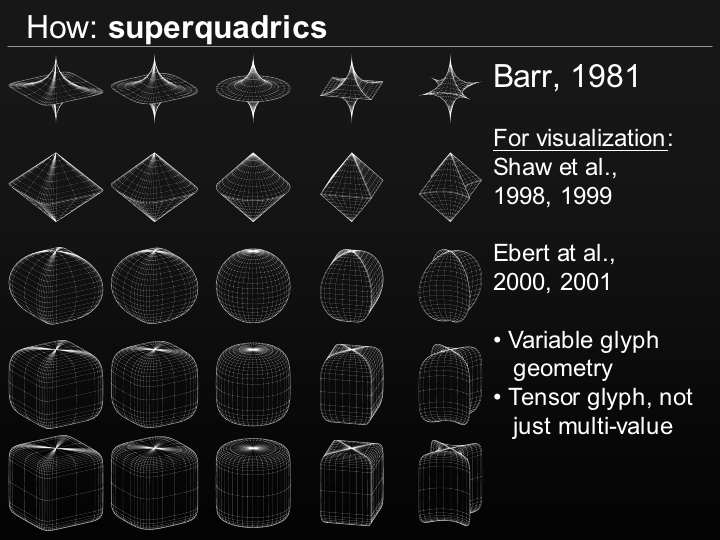
Bounding objects are now quite a common technique for object identification. Unfortunately objects are quite complex, to combat this a particular class of geometric shapes have been developed. This class is superquadratics, and they are defined by functions which resemble those of ellipsoids and other quadrics, however the square is replaced by arbitrary powers.

Quick Run:

A superquadratic function is defined as follows:

$$|x|^r + |y|^s + |z|^t = 1$$

Now scaling can occur, to change the effecct a variable has on the shape. All exponents must be real positive numbers. Now we can see majority of complex shapes can be modeled using these. These functions worked incredibly well for mushroom fitting.

Most Important Tidbits:

• If the exponents are less than 1 you get an octahedron with pointy edges, and concave faces
• If they are exactly 1 you get a regular octahedron
• Between 1-2 you get an octahedron with convex faces and blunt edges
• Exactly 2 is a sphere
• Over 2 and is a cube with rounded edges
• Limit going to infinity makes it a cube